A recent report from the UNESCO Institute of Statistics suggests that many children around the world are lacking the most fundamental numeracy skills. In particular, 38% of 3-5 year-olds in low-income countries are not developmentally on track with Counting (this compares to 19% for middle-income countries and 15% for low-income countries).1 In this piece, our Senior Education Specialist, Fiona Goddard, reveals that there is more to Counting than meets the eye, and shows parents and educators how they can keep track of their child’s progress through each stage of development.
One, two, three, four, five …

Children will start counting by copying counting behaviours modelled by adults. Children’s rhymes, games, and songs have set the stage for the seemingly effortless acquisition of verbal counting – repeating numbers by rote. While teaching children to count up to 10, 20 or even 100 is a start, the mere act of reciting number words does not itself equate to counting.
Counting may seem like a simple concept, but there are actually several distinct counting principles that progressively build toward a child being able to effectively count a group of objects. There are five long-established counting principles2 that children must know in order to be able to count well. Each principle can be made visible once you know what to look for and ask.
The first three principles are considered the ‘how’ of counting as they specify the way in which children must execute a count:
1. The stable-order principle
2. The one-one principle
3. The cardinal principle
The remaining two principles are the ‘what’ of counting as they define what can actually be counted:
4. The abstract principle
5. The order-irrelevance principle
Let’s look at these in more detail.
1. The stable order principle
This involves the child using a list of words to count in a repeatable order. Everyone uses these counting words and they never change. This ordered or ‘stable’ list of counting words known by the child must be at least as long as the number of items to be counted.

2. The one-one principle
Understanding that each object in a group can be counted once. The child says one number, and only one number, for each object being counted.
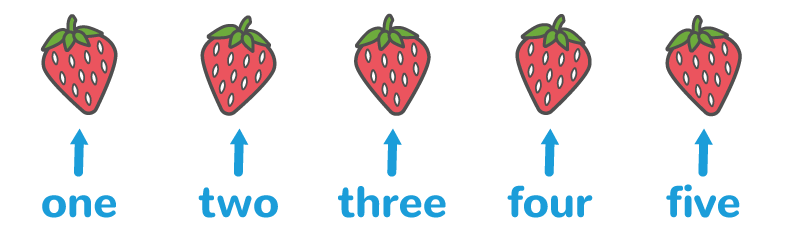
For example, how many strawberries? The child has to point and count each strawberry.
We can promote the development of this skill by regularly counting items during play and everyday life by encouraging children to:
• “Tag” or move items out of the way while counting
• Show quantities on their fingers
3. The cardinal principle
On condition that the one-one and stable-order principles have been followed, the child names the total number of objects in a group according to the last number used in their count. To have grasped this principle, the child needs to appreciate that the final number name is different from the earlier ones in that it not only ‘names’ the final object, signalling the end of the count, but also tells them how many objects have been counted, indicating the numerosity of the set.
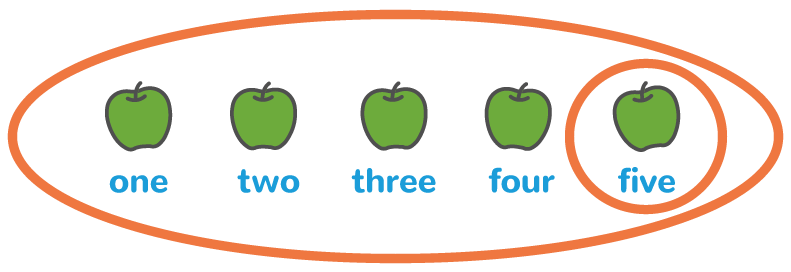
For example: counting five objects and understanding that five signifies the size of the group.
You can explicitly ask the child to show you how many objects there are in the group.
4. The abstract principle
At this stage, the child understands that the preceding principles can be applied to any collection of objects, whether tangible or not. It does not matter what is counted; the way we count is always the same.
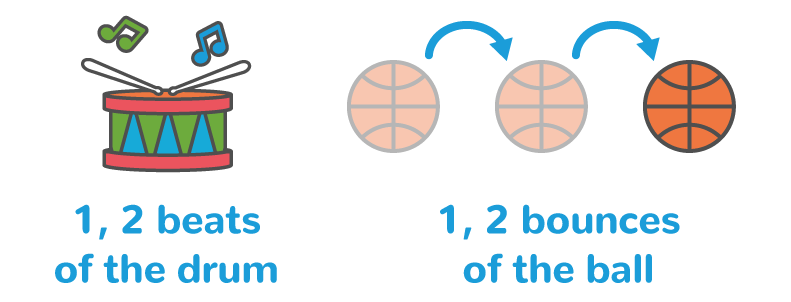
Examples include counting non-tangible quantities such as sounds, actions, words, questions or steps.
5. The order irrelevance principle
Finally, children acquire an understanding of ‘order irrelevance’ when they are able to count a group of items starting from different places.

For example, you can ask the child to count the same set of items from left-to-right, right-to-left, top-to-bottom and bottom-to-top. They should notice and understand that the answer is independent of the counting order.
Final thought
Counting is the building block of number. What this summary demonstrates is that we should not simply be asking whether or not students can count. The question is far more nuanced than that, and the five principles are a useful way to keep track of students’ development on a more granular scale. If you work with children directly, the examples above are a great way of making their thinking visible so that you can fully appreciate how they think about number.
1 Meeting commitments: are countries on track to achieve SDG4? https://unesdoc.unesco.org/ark:/48223/pf0000369009
2 The principal counting principles https://www.ncetm.org.uk/public/files/712850/The+principal+counting+principles.pdf
